前回の手牌です。
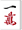
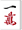
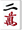
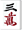
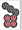
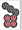
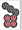
仲間内の麻雀でこれをヤミテンの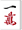で出アガり、3200点（子）と申告すれば、たいそう喜ばれる筈です。
次の局が始まるやいなや、「純チャンが見えなかったの?!」と煽られるかもしれません。
ただ、競技の場合は他の競技者、あるいは審判が指摘し、8000点に修正します。
これが「高点法」の順守なのですが、なぜこのような決まりがあるのでしょうか。
高点法が招く悲劇
競技の場合は大抵、その半荘の結果とは別に、トータルのポイントがあります。
それはある程度多い回数を打たないと実力を測れないという考え方から由来します。
最終1回前までのトータルポイントが
A＋50.0
B＋70.1
C＋30.0
D△150.1
※ルールは順位点が＋30＋10△10△30とする
そして、最終回オーラスを迎えての持ち点が
A 40000（親）
B 37900
C 28100
D 14000
だとします。Cさんは上記の手で見事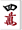
をツモアガりました。
リーチ・ツモ・三暗刻の満貫です。（裏ドラは便宜上、度外視）
満貫をツモアガった場合の得点の変化は
A 40000→36000（2位）
B 37900→35900（3位）
C 28100→36100（トップ）
D 14000→12000（ラス）
となり、順位点を加えたポイントは
A＋16.0
B△ 4.1
C＋36.1
D△48.0
さらに、トータルポイントに加えて
A＋66.0
B＋66.0
C＋66.1
D△198.1
と見事にCさんは先行する二人をかわして優勝をとげます。
しかし、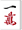をツモった場合にはどうなるでしょうか。ハネ満をツモった場合の得点の変化は
A 40000→34000（3位）
B 37900→34900（2位）
C 28100→40100（トップ）
D 14000→11000（ラス）
と2位、3位が入れ替わります。
その結果、順位点を加えたポイントは
A△ 6.0
B＋14.9
C＋40.1
D△49.0
トータルは
A＋44.0
B＋85.0
C＋70.1
D△199.1
でBさんの優勝になってしまいます。
ここでCさんはこの手は三暗刻なのだ、という主張はできません。
それが、高点法なのです。
では、なぜ自分に都合の良い申告ができないとされているのでしょうか。
もし、自分に都合の良い恣意的な申告を許すと、例えば、差し込み（局の進行狙いでわざと放銃すること）要求で、相手が応じた場合に常に1000点と申告することができてしまいます。
ですので、申告は正しく（＝最も高く）行うことになっているのです。
裏ドラ放棄は許される？
さて、上記の状況でCさんがこの手を作ったとします。
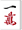
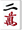
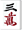
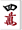
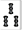
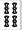
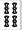
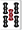
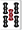
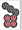ツモ ドラ
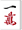を捨ててリーチ、首尾よくをツモりました。
リーチ・ツモ・タンヤオ・ピンフ・ドラ１の満貫達成ですから、裏ドラを見る必要はさらさらありません。
Cさんは、裏ドラをめくらないということはできるのでしょうか？
正解：できない
審判から「ピーピーピー」とホイッスルを鳴らされてしまいます。
理由は高点法の考え方と同じです。
Cさんが、祈るように裏ドラをめくると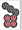が乗りました。
ハネ満になってしまいBさんの優勝です。
競技において、こんなバカげたことがあって良いのでしょうか・・・。
もし、土田さんが提唱する裏ドラ開示ルールであれば、Cさんは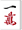ではなく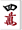を切ってリーチすることができたのです。
ルールの趣旨を考えてみよう
以下は付録ですが、高点法の題材によく次のような手牌が出てきます。
（細かい話はどうでも良いという読者はスルーしてください）
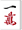
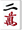
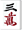
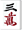
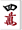
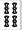
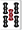
待ちは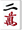
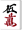ですが、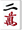をツモった場合の点数（子）はいくらでしょうか？
正解：700・1300
いわゆる「点パネ」ですが、これは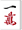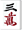のカンチャンをツモったのだから2点付く。の暗刻が8点、ツモの2点に加えて計12点、副底（フーテイ＝基礎点）の20点に加えて32点の一の桁を切り上げて40点。
役はツモ・役牌の2役なので
40×2×2×（2×2）＝640点（子一人の得点）
※（2×2）は場ゾロ
子一人の得点が出れば、それを2倍して親の得点を計算します。
640×2＝1280点
子と親の得点の比が1：2であることを「ヤオアルの法則」と呼びます。
※ヤオは1、アルは2を意味する中国語。ヤオチュー牌は19牌の意。
ただし、そこから10点単位をさらに切り上げるので、700・1300となり結果的に「ヤオアルの法則」は崩れます。
ちなみに101では「ヤオアルの法則」を順守し、子の切り上げ後に2倍するため700・1400という耳慣れない得点が出現します。
と、ここまで説明したところで本題に戻りましょう。
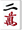をツモってカンチャンに取るというのはどうなの、ということです。
ペンチャン・カンチャン・タンキ待ちに2点を付けるというのは、不利な（悪い）待ちをアガった場合のボーナスです。それがルールの目的ですので、目的に合致していないにもかかわらず、高点法を持ち出して計算するのはあきらかな逸脱だと筆者は考えますが、いかがでしょうか。
解決法としては、待ちが複数ある場合、点は付かないとルールで明示するする以外ありませんね。
